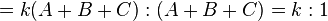20151022
*이문제는 가비의 리 개념을 알고 있으면 풀기 편한 문제 입니다.
*이문제는 dovelet 에 있는 알고리즘 문제입니다.
기울기/slant
프로그램 명: slant
제한시간: 1 초
엑스 형은 와이 다.
와이는 엑스 보다 용돈을 매 달 일정한 배수 만큼의 용돈을 더 받는다.
3 배 더 받는경우
- 엑스가 300 원 받으면 와이는 900 원
- 엑스가 400 원 받는 달은 와이는 1200 원
그런데 와이가 용돈이 적다고 불만이 많아 받은 금액에서 일정한 액수의 돈을 더 주기로 했다.
100 원 더 준다면
위 예에서는 1000 원 , 1300 원을 받게 된다.
엑스는 와이가 자기보다 용돈을 몇 배 더 받는지가 궁금했지만 형은 가르쳐 주지 않아 이렇게 질문을 했다.
"그러면 형님아 지난 달에 얼마를 , 이 번달에 얼마를 받았는지만 가르쳐 주"
와이 " 가르쳐 줄테니 몇 배 더 받는지는 알려고 하지마!!!"
엑스는 다음의 아이디어로 몇 배를 더 받는지를 알고자 한다.
"비가 같은 것 끼리 빼고 , 더하면 비가 같다 . 그런데 이 경우 빼 버리면 얹어 주는 돈이 없어지니 원하는 결과를 얻을 수 있다"
입력
동생과 형의 받는 용돈 두 번의 금액이 입력으로 주어진다.
출력
몇 배가 되는지를 출력한다. 정수배가 된다는 것은 보장된다.
입출력 예
입력 300 1000 400 1300 출력 3 100
채점데이터:cube
문제 풀이
1) 풀이
import java.io.PrintStream;
import java.util.Scanner;
public class Main {
Scanner sc = new Scanner(System.in);
PrintStream p = System.out;
int underbrother1, olderbrother1, underbrother2, olderbrother2;
public static void main(String[] args) {
Main ma = new Main();
ma.input();
ma.result();
}
void input(){
underbrother1 = sc.nextInt(); //동생
olderbrother1 = sc.nextInt(); //형
underbrother2 = sc.nextInt(); //동생
olderbrother2 = sc.nextInt(); //형
}
void result(){
int x = (olderbrother2 - olderbrother1)/(underbrother2 - underbrother1);
p.println(x + " " + (olderbrother1-underbrother1*x));
}
}
*짧게 코딩하는것도 좋지만 저는 함수와 객체 지향개념을 쓰고 싶어서 이렇게 코딩 했습니다.
생각하는 시간이 좀 걸려던 문제 입니다. 대다수가 '가비의 리' 개념을 사용해서 쉽게 풀었습니다.
저는 '가비의 리' 개념을 몰라서 미지수 2개 식2개 로 미지수를 구하는 방식으로 풀었습니다.
우선 동생돈 형돈 값이 총 2번 입력 되어집니다.
방정식을 만들어 보면
형돈 = 동생돈 * 배수 + 추가돈
입니다.
이 방정식에서 형돈과 동생돈을 알려주므로 미지수는 배수와 추가돈 이죠
입력 값을 예로 풀어볼게요.
예)
300 1000
400 1300
1000(형돈) = 300(동생돈)*X(배수) + a(추가돈)
1300(형돈) = 400(동생돈)*X(배수) + a(추가돈)
공통 미지수인 a(추가돈)만 남기고 수식을 정리하면
1000 - 300*X = a
1300 - 400*X = a
그렇다는건
1000 - 300*X = 1300 - 400*X
라는거죠 미지수 X 만 남기고 수식을 정리하면
400*X - 300*X = 1300 - 1000
(400 - 300)*X = 1300 - 1000
X = (1300 - 100)/(400 - 300)
이렇게 됩니다. 미지수 X 배수 를 알 수 있습니다.
추가 돈은 동생돈에서 배수를 곱한걸 형돈에서 빼주면 알 수 있겟죠
저는 나름 고민하다가 이런식으로 풀었습니다. 그런데 '가비의 리' 개념을 알면 더 쉽게
풀엇을것 같네요. 아래는 가비의 리 개념 입니다.
가비의 리
'알고리즘(dovelet 문제풀이) > 1층' 카테고리의 다른 글
| angle/open(angle 알고리즘) (0) | 2015.10.22 |
|---|---|
| maxandmin/maxandmin(maxandmin 알고리즘) (0) | 2015.10.22 |
| 버터 먹기/butter(버터 먹기 알고리즘) (2) | 2015.10.22 |
| 사탕/coci_slatkisi(사탕 알고리즘) (2) | 2015.10.21 |
| 논문인용/coci_faktor(논문인용 알고리즘) (0) | 2015.10.21 |